Подбор сечения металлической балки

Подбор сечения металлической балки

Бывают случаи, когда деревянные балки для междуэтажных или чердачных перекрытий использовать экономически не выгодно. Например, когда пролет слишком большой и поэтому для его перекрытия требуются деревянные балки большого сечения. Или когда у Вас есть хороший знакомый, который торгует не пиломатериалом, а металлопрокатом.

1. Калькулятор

2. Инструкция к калькулятору

В любом случае не лишним будет знать во сколько может обойтись перекрытие, если использовать металлические балки, а не деревянные. И в этом Вам поможет данный калькулятор. С его помощью можно рассчитать требуемые момент сопротивления и момент инерции, которые для подбора металлических балок для перекрытия по сортаментам из условия прочности и прогиба.

Рассчитывается балка перекрытия на изгиб как однопролетная шарнирно-опертая балка.

Калькуляторы по теме:

• Сбор нагрузок на балки перекрытия онлайн.

Исходные данные

Условия эксплуатации:

Длина пролета (L) — расстояние между двумя внутренними гранями стен. Другими словами, пролет, который перекрывают рассчитываемые балки.

Шаг балок (Р) — шаг по центру балок, через который они укладываются.

Вид перекрытия — в случае, если на последнем этаже Вы жить не будете, и он не будет сильно захламляться милыми Вашему сердцу вещами, то выбирается «Чердачное», в остальных случаях — «Междуэтажное».

Длина стены (Х) — длина стены, на которую опираются балки.

Характеристики балки:

Длина балки (А) — самый большой размер балки.

Вес 1 п.м. — данный параметр используется как бы во втором этапе (после того, как Вы уже подобрали нужную балку).

Расчетное сопротивление Ry — данный параметр зависит от марки стали. Например, если марка стали:

• С235 — Ry = 230 МПа;
• С255 — Ry = 250 МПа;
• С345 — Ry = 335 МПа;

Но обычно в расчете используется Ry = 210 МПа для того, чтобы обезопасить себя от разного рода «форс-мажерных» ситуаций. Все-таки в России живем — привезут металлопрокат из стали не той марки и все…

Модуль упругости Е — этот параметр зависит от вида металла. Для самых распространенных его значение равно:

• сталь — Е = 200 000 МПа;
• алюминий — Е = 70 000 МПа.

Нагрузка:

Значения нормативной и расчетной нагрузок указываются после их сбора на перекрытие.

Цена за 1 т — стоимость 1 тонны металлопроката.

Результат

Расчет по прочности:

Wтреб — требуемый момент сопротивления профиля. Находится по сортаменту (есть ГОСТах на профили). Направление (х-х, y-y) выбирается в зависимости от того, как будет лежать балка. Например, для швеллера и двутавра, если Вы хотите их поставить (т.е. больший размер направлен вверх — [ и Ι), нужно выбирать «x-x».

Расчет по прогибу:

Jтреб — минимально допустимый момент инерции. Выбирается по тем же сортаментам и по тем же принципам, что и Wтреб.

Другие параметры:

Количество балок — общее количество балок, которое получается при укладки их по стене X с шагом P.

Общая масса — вес всех балок длиной А.

Стоимость — затраты на покупку металлических балок перекрытия.

Расчет металлической балки перекрытия на прогиб и на жесткость

Металлические балки двутавровые

Кроме повсеместно ведущегося строительства многоэтажных зданий с большим числом квартир, широкое распространение получило сооружение частных домов, причем не только небольших одноэтажных, но и довольно крупных, с двумя и более этажами, иногда и с мансардой наверху или обитаемым чердаком.

Для таких домов уже не подходит каркасный метод; материалом часто служит, вместо дерева, кирпич или железобетон.

Возведение крупных частных домов должно вестись по всем правилам строительной науки, так как ошибки при проектировании или воплощении проекта могут привести к нежелательным последствиям.

Если строящийся дом представляет собой капитальное здание – из бетона, кирпича, шлакоблока, то для потолочных перекрытий, межэтажных и чердачных, целесообразно применить железобетонные плиты. Наиболее подходящий тип каркаса, способный выдержать вес таких перекрытий, – это каркас, элементом которого является металлическая балка двутаврового профиля.

Именно этот вид проката, установленный своей стенкой вертикально, обладает наибольшей несущей способностью. Естественно, фундамент и стены дома при этом должны быть достаточной прочности, чтобы выдерживать дополнительный вес от 0,5 до 1 тонны – столько металла, в зависимости от количества балок и номера профиля может понадобиться для потолочного перекрытия.

Чтобы избежать лишних затрат и лишнего веса каркаса потолка, а также не допустить обрушения или значительного прогиба балок, необходимо заранее рассчитать их параметры и по результатам расчета подобрать нужный прокат. Расчет сводится к вычислению следующих величин: требуемого момента сопротивления и минимального момента инерции сечения балки, а исходя из последнего – максимального относительного прогиба.

Примечание

Расчет ведется по двум характеристикам – на прочность и на жесткость. По полученным значениям момента сопротивления и момента инерции в таблицах ГОСТ находят требуемый номер проката.

Исходные данные для расчетов

Для каркаса потолочных перекрытий малогабаритных частных домов обычно используется двутавр 10 – 20 номеров. Характеристики этих профилей приводятся в ГОСТ 8239-72 – их линейные размеры, площади сечения, максимальные моменты сопротивления по вертикали Wy и минимальные моменты инерции Jy.

Необходимо знать тип плит, которые будут опираться на балочный каркас, а также размеры несущего периметра дома. Можно применить пустотные железобетонные плиты ПК-12-10-8 (1180 х 990 мм, масса 380 кг), а размеры дома взять 4,5 х 6 м.

Балки укладываются вдоль короткой стены; шаг укладки при таком размере плит равен 1000 мм (стыки плит совпадают с продольными осями балок, при минимальном зазоре 1 см).

Это потребуется для расчета распределенной нагрузки, и исходя из нее – линейной нагрузки на балку, вес самой балки по сравнению с распределенной нагрузкой мал, и при вычислении линейной нагрузки им можно пренебречь.

Распределенная нагрузка при таком типе плит будет равна 325 кгс / м2. К этому надо добавить нагрузку возможных перегородок на верхней стороне перекрытия (75 кгс / м2) и возможную временную нагрузку (200 кгс / м2). В итоге нагрузка, распределенная по площади:

Q = 325 + 75 + 200 = 600 кгс / м2,

а линейная нагрузка

q = Q * p = 600 кгс / м = 6 кгс / см.

Эта величина используется в дальнейших расчетах.

Расчет на прогиб

Изгибающий момент для каждой балки вычисляется, исходя из величины линейной нагрузки q, шага укладки балок p и длины перекрываемого пролета L. Так как балки укладываются вдоль короткой стороны, то L = 4,5 м = 450 см (конечно, сами балки длиннее – около 5 м, так как опираются на стены, но шарнирными опорами для них служат именно внутренние края стен).

Искомая величина момента, в таком случае:

My = (q * L2) / 8 = 6 * 4502 / 8 = 151875 кгс * см.

Максимальный момент сопротивления сечения балки можно рассчитать, разделив изгибающий момент на расчетное сопротивление стали – например, марки С235, равное 2150 кгс / см2:

Расчеты металлической балки перекрытия на прочность и прогиб, онлайн-калькулятор

Несмотря на бушующий в мире экономический кризис, который, к сожалению, затронул и нашу страну, строительство объектов различной важности продолжает производиться. При этом, в последнее время получило новый толчок развития именно промышленное строительство, однако, потребность жителей страны в жилых квадратных метрах не уменьшилось.

Сегодня в строительстве промышленных и гражданских объектов повсеместно применяются металлические балки перекрытия, которые повышают несущую способность всей конструкции.

Описание

Стальные балки перекрытия представляют собой металлический брус определённой длины и определённой формы поперечного сечения. Как правило, металлические балки исполняются из высокопрочной стали марки Ст 5 с формой поперечного сечения типа двутавр и швеллер.

Балки производятся именно в таких формах поперечного сечения, потому что расчёт показывает, что такая форма является более экономически выгодной по сравнению с другими геометрическими фигурами.

Кроме того, расчёты показывают, что балка именно двутаврогого сечения лучше всего воспринимает давление и такие нагрузки, как изгиб, кручение и их совместное действие.

Продолжая перечислять преимущества двутавровых балок, можно отметить немаловажный факт того, что такая форма сечения помогает уменьшить вес конструкции.

Это помогает снизить нагрузку, например, на стены и фундамент здания, если в межэтажном перекрытии использовать металлические балки перекрытия. Также, из преимуществ можно отметить простоту монтажа любой конструкции из балок, скорость выполнения работ.

Для большей экономии использования металла и для облегчения всей конструкции существует сортамент балок двутаврового и швеллерного поперечного сечения. Площадь сечения изменяется от минимальной равной 12 кв. см до максимальной 234 кв.

см, соответственно, для номеров профиля 10 и 70б.

Все значения площадей и массы профиля представлены в таблицах ГОСТ 8239-72. Чтобы её произвести, необходимо произвести расчёт профиля по прочностным характеристикам и вычислить подходящую площадь.

Точная методика представлена ниже.

Таким образом, видно, что в качестве бруса перекрытия стоит использовать именно стальные балки, так как они во многом выигрывают по сравнению с конкурирующими материалами.

Область применения

Чаще всего, двутавровые балки применяются в промышленном строительстве, а именно, в случае возведения зданий с большими пролётами между опорами.

Благодаря своим механическим характеристикам и стойкости к динамическим воздействиям, металлический брус используют при возведении дорог и мостов и в других случаях необходимости возведения конструкций, выдерживающих большие нагрузки подобного характера.

В последнее время, стальные двутавровые балки стали применять в качестве элемента декора в квартирах и офисах. После покраски, металлическая балка может выглядеть эстетично и иметь практическое применение в бытовом хозяйстве.

Расчет

Чтобы произвести выбор металлического бруса для той или иной конструкции, которая будет нести определённую нагрузку, необходимо произвести расчёт балки на прочность при изгибе. Это можно сделать, рассчитав все параметры самостоятельно по известной методике или воспользоваться онлайн-калькулятором.

Для выбора балки перекрытия, делают проверку из условия на прочность, где максимальная прочность стали должна быть больше суммы отношений максимального изгибающего момента в точке действия той или иной нагрузки к осевому моменту, и поперечных сил и площади поперечного сечения в максимально нагруженной точке.

Для определения всех неизвестных параметров этого условия, вычисления проводят поочерёдно.

Сначала определяют максимально нагруженный участок балки. Для этого, строят эпюру поперечных сил и изгибающих моментов. Чтобы построить эпюру, необходимо вычислить все суммарные изгибающие моменты и поперечные силы, действующие на балку, по участкам.

Как правило, в случае металлического бруса перекрытия, расчётную схему заменяют балкой, лежащей на двух шарнирных опорах. В этих опорах возникают реакции сопротивления, у которых необходимо определить их условия:

Когда реакции определены, балку разбивают на участки по опорам. Первый участок находится от одного конца балки до опоры, второй участок располагается между опорами, третий за последней опорой и так далее. Необходимо знать, что если на одном участке имеется точка изменения нагрузки, то её нужно выделить в отдельный участок.

После того, как участки определены, строятся эпюры поперечных сил и изгибающий моментов, и определяется нагруженный участок. Далее, вычисляется осевой момент сопротивления сечения:

По вычисленному параметру производят выбор номера двутавра из сортамента. На этом расчёт балки считается оконченным.

Онлайн

Рассчитывать металлическую балку и производить её выбор вручную довольно трудоёмко и занимает время, которое не всегда можно выделить занятому человеку. Поэтому, стоит довериться расчётам профессионалов.

Но, если заказчик строительства сомневается в экономической целесообразности произведённого строителями расчёта, можно произвести быстрый автоматический расчёт при помощи сайтов, предлагающих данный товар.

Одним из примеров такого калькулятора может быть портал http://svoydomtoday.ru/building-onlayn-calculators/111-raschet-metallicheskoy-balki-perekritiya.html, который предлагает, находясь на сайте, рассчитать расход материала и выбрать балку из сортамента.

Данный калькулятор требует введения следующих исходных данных:

1. Сначала нужно ввести условия эксплуатации металлической балки.
2. После этого характеристики предварительно выбранной металлической балки.
3. Указать нормативную и расчётную нагрузку на балку и произвести расчёт.

В результате, получается минимально возможный при заданных условиях момент сопротивления балки. Из полученного момента можно выбрать балку по таблице сортамента.

Так же определяется минимально допустимый момент инерции, по которому можно выбрать номер профиля из сортамента. Если для строительства в первую очередь важно не допустить прогиб балки, тогда стоит выбирать балку исходя из полученного момента инерции.

Пример расчета

Металлической балки перекрытия:

Расчет несущей способности:

1. Чтобы рассчитать несущую способность одной балки нужно из таблицы сортамента выбрать момент осевого сопротивления и по формуле вычислить максимально допустимый изгибающий момент:
2. Отсюда можно вычислить максимально допустимую равнораспределённую нагрузку на однопролётную балку.

Расчет сечения металлических балок:

1. Для расчёта необходимого сечения металлической балки можно воспользоваться формулой расчёта момента сопротивления сечения.
2. После вычисления результата, определить площадь сечения нужно по сортаменту фасонного профиля, выбрав при этом номер двутавра с ближайшим большим значением момента сопротивления.

При расчёте металлической балки пролёта необходимо отнестись ко всему ответственно и внимательно, потому что от расчёта зависит срок эксплуатации здания и его возможная нагрузка. Здания, построенные по ошибочным расчётам, могут разрушиться в любой момент, унеся за собой много жизней.

Металлические балки перекрытия

Кроме того, металлические балки могут быть любой длины и даже не из цельного металлопроката, а сваренными из отдельных кусков. И хотя такое соединение следует выполнять согласно отдельному расчету, но тем не менее это позволяет минимизировать отходы при устройстве перекрытия, а значит и сэкономить.

И еще одна очень важная особенность металлических балок перекрытия — такие балки могут использоваться для устройства перекрытия сразу над двумя, тремя и больше помещениями. Т.е. металлическая балка может быть и двухпролетной и трехпролетной. И хотя в малоэтажном частном строительстве такое случается не часто, тем не менее подобный вариант мы тоже рассмотрим.

Начнем с более простого — упрощенного расчета металлической балки перекрытия однопролетной с шарнирными опорами из цельного металлопроката. Как произвести наиболее полный расчет согласно действующих нормативных документов, рассказывается отдельно.

Дано:

Планируется деревянное перекрытие по металлическим балкам. Шаг балок (расстояние между центрами тяжести поперечных сечений балок) — 1 метр. Расстояние между стенами в свету l = 5.

4 метра — это пролет балки.

Нагрузка на балку — это собственный вес балки, который мы пока не знаем, вес конструкции перекрытия по металлическим балкам и все остальные временные нагрузки (мебель, оборудование, люди и т.п.).

Если перекрытие будет не очень тяжелым, например, черновой пол из досок по лагам, выравнивающий листовой материал из продуктов обработки древесины (фанера, ДСП, ОСП и др.

), а сверху плитка ПВХ, линолеум или ковролин, кроме того тяжелых перегородок по перекрытию из кирпича или шлакоблока также не планируется, то при расчетах балки можно использовать проверенную временем величину плоской равномерно распределенной нагрузки — 400 кг/м2. Т.е. при шаге балок 1 м линейная равномерно распределенная нагрузка на балку составит:

q = 400·1 = 400 кг/м.

Примечание: при шаге (расстоянии между осями) балок 0.5 м линейная равномерно распределенная нагрузка составила бы q = 400·0.5 = 200 кг/м.

Требуется:

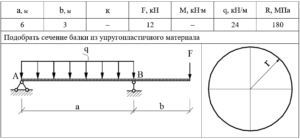
Подобрать сечение металлических балок.

Решение:

1. Расчет на прочность (по первой группе предельных состояний).

1.1 Максимальный изгибающий момент для бесконсольной балки на шарнирных опорах, , на которую действует равномерно распределенная нагрузка, будет посредине балки:

Мmax = ql2/8 = 400·5.42/8 = 1458 кгм или 145800 кгсм

1.2 Требуемый момент сопротивления:

Wтреб = Мmax / Ry = 145800/2100 = 69.43 см3

где Ry — расчетное сопротивление стали. Ry = 2100 кгс/ см2 (210 МПа)

Примечание: Вообще-то расчетное сопротивление стали следует узнавать у производителя того самого металлопроката, который вы собираетесь использовать.

1.3. Если в качестве балкок перекрытия будут использоваться двутавры, то согласно сортаменту нашим условиям удовлетворяет двутавр №14 с моментом сопротивления Wz = 81.7 см3.

Примечание: При определении момента сопротивления, как и момента инерции, важно не спутать оси координат, относительно которых данные геометрические характеристики определяются. В сортаментах эти оси могут называться по-разному.

У меня ось, относительно которой в поперечном сечении возникают нормальные сжимающие и растягивающие напряжения обозначена как z, в сортаментах эта ось может быть обозначена как х.

Но важно не название, а принцип, когда мы определяли максимальный изгибающий момент, действующий на поперечное сечение балки, то длина балки l измерялась по оси х, высота балки по оси у, а ширина балки по оси z (хотя я обо всем этом не рассказывал, чтобы не погрязнуть в деталях). Таким образом, какой сортамент Вы бы не взяли, и как ни называлась бы ось, главное, чтобы по этой оси определялась ширина балки. Почему это так важно, рассказывается отдельно.

2. Определение прогиба (расчет по второй группе предельных состояний).

Для однопролетной балки на шарнирных опорах, на которую действует равномерно распределенная нагрузка, максимальный прогиб будет посредине балки и составит:

fmax = 5ql4/(384EIz) = 5·4·5404/(384·2·106·572) = 3.87 см

где q — нагрузка выраженная в кг/см;

l — длина пролета в см;

E — модуль упругости, для стали Е = 2·105 МПа или 2·106 кг/см2

Iz — момент инерции согласно сортаменту для выбранного швеллера.

По требованиям СНиПа 2.01.07-85* «Нагрузки и воздействия» максимальная величина прогиба для балок перекрытия, открытого для обзора, не должна превышать 1/200 пролета (при l = 6 м), т.е. в нашем случае прогиб должен быть не более 540/200 = 2.7 см. Это требование не выполнено, поэтому мы, преобразовав формулу прогиба, можем определить требуемый момент инерции поперечного сечения:

Iz = 5ql4/(384Ef) = 5·4·5404/(384·2·106·2.7) = 820.1 см4

Этому требованию удовлетворяет двутавр №16 с моментом инерции Iz = 873 см4.

Примечание: Если по каким либо причинам и такой прогиб кажется вам чрезмерным, то вы можете подобрать сечение, исходя из своих соображений о допустимой величине прогиба.

Так как принятое нами перекрытие является достаточно легким, его следует проверить дополнительно на физиологический прогиб, т.е. на прогиб, который будет возникать при ходьбе по минимально загруженному перекрытию. В этом случае максимально допустимая величина прогиба составит:

fф = g(p + p1 + q)/(30n2(bp + p1 + q))

где g — ускорение свободного падения g = 9.81 м/с2;

р — значение нормативной нагрузки от людей, которые возбуждают колебания перекрытия. р = 25 кг/м2 — при расчете перекрытий в квартирах и домах;

р1 — значение пониженной нормативной нагрузки на перекрытие, принимается равным р1 = 150·0.35 = 52.5 кг/см2 для перекрытий в жилых зданиях;

q — значение нормативной нагрузки от веса рассчитываемого элемента, в данном случае металлической балки перекрытия и опирающихся на него элементов пола (лаги, половая доска, и др.). В данном случае нагрузка от веса металлической балки согласно все тому же сортаменту составит qб = 15.

9 кг/м2, нагрузка от плитки ПВХ и фанеры толщиной 1см qп = 6 кг/м2 (при объемном весе фанеры около 550 кг/м3), нагрузка от досок толщиной 2.7 см qд = 500·0.027 = 13.5 кг/м2, нагрузка от лаг сечением 5х10 см, уложенных с шагом 50 см qл = 2·500·0.05·0.1 = 5 кг/м2 , тогда q = 15.

9  +6 + 13.5 + 5 = 40.4 кг/м2;

Примечание: вообще-то нагрузку от лаг более правильно рассматривать не как равномерно распределенную, а как несколько сосредоточенных, но так как лаг у нас будет больше 10, то такое уточнение будет не очень актуальным и потому мы будем рассматривать нагрузку от лаг, как равномерно распределенную даже без использования соответствующего коэффициента перехода.

n – частота приложения нагрузки при ходьбе человека, как правило принимается n = 1.5 Гц (1/с);

b – коэффициент, равный 125√Q/(αpal)

где Q — нагрузка от человека, принимаемая равной 80 кг (во всяком случае так рекомендуют СП, хотя сейчас более актуальной может быть нагрузка и 100 кг);

α — коэффициент, учитывающий перераспределение нагрузки; для элементов конструкций, рассчитываемых как балки, принимается равным 1,0;

а – шаг балок (лаг, ригелей), ширина рассчитываемых плит (настилов), в нашем случае а = 1 м;

l – расчетный пролет элемента конструкции, l = 5.4 м.

В итоге значение коэффициента b составит

b = 125√80/(1·25·1·5.4) = 96.225

тогда

fф = 9.81(25 + 52.5 + 40.4)/(30·1.52(96.225·25 + 52.5 + 40.4)) = 0.00686 м или 0.686 см

Теперь осталось определить, каким будет прогиб при динамической нагрузке, возникающей при ходьбе по перекрытию:

fд = 2Ql3/48EI = 2·80·5403/48·2·106·873 = 0.3 см

Как видим, прогиб от динамической нагрузки, создаваемой человеком, значительно меньше предельно допустимого нормами. Однако, если вы собираетесь по перекрытию не только спокойно ходить, но еще бегать, прыгать, ронять штанги и другие тяжелые предметы, то это следует учесть при расчете.

Пример расчета металлической двухпролетной балки перекрытия

Для наглядности рассмотрим металлическую балку, перекрывающую два равных по длине пролета l = 5.4 м при той же нагрузке. Максимальный изгибающий момент для такой балки будет возникать на средней опоре и составит все те же 145800 кгсм. А вот максимальный прогиб для такой балки будет меньше и составит:

fmax = ql4/(185EIz) = 4·5404/(185·2·106·572) = 1.61 см

Это означает, что двухпролетную металлическую балку мы можем делать из двутавра №14, который не подошел нам при расчете однопролетной балки по второй группе предельных состояний.

Конечно же длины пролетов у двухпролетных балок далеко не всегда бывают одинаковыми и в таких случаях для определения максимальных моментов и прогибов можно воспользоваться соответствующими уравнениями.

Подбор сечения двутавра — все тонкости от А до Я

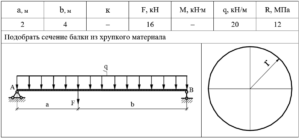
Балка двутавровая или просто двутавр – один из наиболее широко применяемых видов черного фасонного металлопроката. Главное его отличие – сечение в форме буквы «Н». Зачастую возникает необходимость выполнить подбор сечения двутавра. Как это сделать правильно? Читайте далее в нашей статье.

Начнем с общих параметров, чтобы определить основные критерии выбора сечения. Сначала нужно понять что такое двутавр и каковы его основные характеристики.

Итак, двутавр это вид изделий, состоящий из двух полок и соединяющей их стенки. Стенку называют шейкой, полки располагаются параллельно друг другу.

Именно шейка и полки образуют профиль сечения двутавра, о котором и идет речь. Думаем, понятно.

Несколько важных моментов влияющих на выбор сечения двутавра. Первый – материал изготовления и технология производства. Двутавр может изготавливаться из различных материалов, в статье поговорим о металлопрокате. Второй – технология производства, либо сварная, либо горячекатаная двутавровая балка. И третий – предназначение изделий (нагружаемые или ненагружаемые конструкции).

Подбор сечения двутавра – сортамент, ключевые моменты

Исходя из того что двутавр – две полки, соединенные шейкой, определяются размеры сечения по таким параметрам как:

• общая высота профиля (включая длину шейки и толщину двух полок);
• высота стенки двутавра;
• общая ширина каждой из полок;
• ширина одной части полки от шейки к краю, называется свесом;
• толщина шейки (стенки);
• толщина полки проката с гранями, расположенными параллельно;
• средняя толщина полки проката с уклоном внутренних граней;
• радиус закругления перехода от полки к стенке, он же радиус сопряжения, внутреннего закругления;
• радиус закругления полки (ее кромки).

Вот эти значения и определяют подбор сечения двутавра. Ряд из них указан в маркировке, об этом ниже.

Отметим один важный, ключевой момент. Выбор сечения двутавра напрямую зависит от государства, на территории которого будет применяться двутавровая балка.

Немного истории

Не нам судить, но на территории России возникла интересная, парадоксальная ситуация. Суть вопроса в том что двутавр по наклону внутренних граней подразделяется на две группы. Первая – с параллельными внутренними гранями. Вторая – с уклоном внутренних граней. Характеристики (площадь сечения, масса и другие) и эксплуатационные параметры, предназначение зачастую совершенно разные.

Во времена Советского Союза сортамент первой группы определял ГОСТ 26020-83. Сортамент второй группы устанавливался ГОСТ 8239-89 (еще ранее ГОСТ 8239-72). С мая 2018 года в России действует свой национальный стандарт – ГОСТ Р 57837-2017.

Он определяет технические условия, а вот тут внимательно, для двутавра с параллельными гранями полок. И что вполне естественно, заменяет ГОСТ 26020-83. Приказ Росстандарта от 30.11.2018 N 1047-ст.

Пункт первый четко указывает что ГОСТ 8239-89 заменен на ГОСТ Р 57837-2017.

В результате двутавр с уклоном внутренних граней в России оказался вне закона, нет такого и все. На рынке такой прокат есть, а использовать в строительстве официально нельзя.

Других ГОСТов для двутавра с уклоном внутренних граней в России нет. Если не считать специальный прокат (ГОСТ 19428-74) и изделия из цветного проката. Но ГОСТ Р 57837-2017 – это российский национальный стандарт.

В ряде государств СНГ ГОСТ 26020-83 и ГОСТ 8239-89 действуют.

Выбор сечения двутавра – основные расчеты

Помимо сортамента, о нем поговорим детальнее далее, выбор сечения двутавра должен основываться на расчетах. Тут два важных определяющих критерия. Первый – действующие СНиП. Второй – такая наука как «Сопротивление материалов», сокращенно сопромат.

Сечение двутавра рассчитывается исходя из его предназначения и предполагаемых статических и динамических нагрузок. То есть тех нагрузок, которые будут воздействовать на конструкцию. Учитывается развитие пластических деформаций в наиболее нагруженном сечении.

Лекцию по сопромату читать не будем. Остановимся на основных моментах.

Величина сопротивления

Сечение двутавра зависит от величины нужного момента его сопротивления. Многое находится в зависимости от марки стали, ее расчетного сопротивления и корректирующего коэффициента. Рассчитываются такие параметры как:

• высота сечения, в зависимости от пролета балки, условий наименьшего расхода стали, обеспечения требуемой жесткости;
• толщина стенки;
• геометрические характеристики сечения, исходя из момента сопротивления и момента инерции.

Толщина стенки

Под обеспечением требуемой жесткости следует понимать расчеты с учетом полного использования несущей способности материала. Отталкиваться надо от условий обеспечения предельного прогиба. Толщина стенки рассчитывается с использованием различных методик, включая:

• эмпирическую формулу;
• исходя из условий прочности шейки на срез;
• исходя из условий обеспечения местной устойчивости шейки, без укрепления ее дополнительным продольным ребром жесткости.

Обязательно нужно выполнять проверку сечения двутавра. Наиболее важно на прочность по нормальным напряжениям, возникающим в поперечном сечении балки, и на жесткость.

Инженерного образования нет, сопромат – темный лес, требуется выбрать сечение двутавра для несущих, нагружаемых конструкций? Воспользуйтесь услугами квалифицированного инженера или специальным программным обеспечением, введя все исходные данные.

Если конструкции ненагружаемые, то при выборе сечения двутавра расчет нагрузок не так критичен.

Рекомендуем к прочтению:

Широкополочный двутавр: применение и виды

Для «своих» все секреты про двутавры сортамент СТО АСЧМ 20-93

Сортамент и сечение двутавра – ГОСТ Р 57837-2017

Не будем затрагивать тему двутавра с уклоном внутренних граней полок. Раз уж так повелось на Руси использовать только ГОСТ Р 57837-2017, пусть будет ГОСТ Р 57837-2017. Отметим лишь одно.

В прайсах помимо него могут быть указаны все те же ГОСТ 26020-83 и ГОСТ 8239-89. Ах да, есть еще и СТО АСЧМ 20-93, на него тоже ссылаются. Но он отменен на основании информационного письма ТК375/ГР-57837 от 11.

04.2018 года.

Разговор у нас пойдет о выборе сечения для горячекатаного двутавра с параллельными гранями полок. Возьмем за основу сортамент этого вида фасонного черного металлопроката. Но прежде о маркировке двутавра. Она состоит из букв и цифр. Первая цифра обозначает высоту профиля в сантиметрах. Этот параметр называется номером, цифра от 10 до 100.

Следом идет буква. Она указывает на тип в зависимости от условий работы и соотношение размеров. Именно соотношение размеров в полной мере влияет на сечение двутавра. Оттого на типах двутавра остановимся детальнее далее. И еще в маркировке встречается цифра после буквы. Она указывает на профилеразмер в данной серии (по толщине стенки и полки).

Это тоже влияет на сечение.

В качестве примера маркировки 12Б1. Двутавр высотой 12 сантиметров, балочный нормальный, первого профилеразмера.

Какие существуют типы двутавра

О профилеразмерах, соотношении толщины полки и балки, говорить не будем. Это очень важный параметр при выборе сечения двутавра.

Но у одного производителя их бывает до 200 и постоянно количество растет. Все зависит от настроек и характеристик прокатного стана. Описать все в рамках одной статьи невозможно.

Это каталожные данные, причем по каждому металлургическому предприятию в отдельности.

Теперь о типе двутавра и характерных особенностях сечения. Он делится на несколько групп:

• балочный (о нем ниже);
• колонный, характерная черта сечения – высота равна или близка ширине полок, толщина полок увеличенная;
• свайный, сечение с высотой равной или близкой ширине полок, толщина стенки и полки равны.

Теперь о балочном типе двутавра, их два. Первый – нормальный. Характерная черта сечения – ширина полок меньше чем высота профиля. Толщина стенок минимальная. Второй – широкополочный, с увеличенной шириной полок.

Подбор сечения профиля для специального горячекатаного профиля будет отличаться. Во многом это определяется уклоном внутренних граней полок. ГОСТ 19425-74 еще ГОСТом Р 57837-2017 заменить гениальная мысль не пришла в головы (шутка).

Если кратко, то существует два основных вида специальной двутавровой балки. Первый – М (подвесная, монорельсовая). Соотношение основания двутавра к ширине полок примерно 2/1 или 3/1. С – для армирования стволов шахт.

Сечение отличается значительным уклоном внутренних граней полок.

Обращайте внимание что все еще есть на рынке и двутавровая балка У. Буква указывает на то что это узкополочный прокат. Характерная черта сечения – узкие полки.

И последний тип горячекатаного двутавра – Д. Это обозначает дополнительный. По ГОСТ Р 57837-2017 маркируется как ДК и ДБ. Изготавливается по требованиям заказчика. Какое нужно сечение, такое и сделают под заказ.

Особенно актуально когда стоит сложная, нетривиальная инженерная задача при проектировании уникальных металлоконструкций. Среди характерных черт сечения – ширина полки. Она меньше чем ширина полки у широкополочного двутавра.

Но при этом ширина полки двутавра Д меньше чем ширина полки у двутавра нормального типа. Хотя бывают и исключения.

Подводя итог скажем так. Подбор сечения двутавра определяется сложными расчетами. Форма профиля зависит от основных параметров проката и определяет его тип. Иногда характеристики типа определяют вид сечения. С особой тщательностью надо выполнять выбор сечения двутавра для нагруженных конструкций. Остались вопросы? Требуется двутавровая балка? Обращайтесь!

Расчет металлической балки на прогиб: учимся составлять формулы

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Что такое прогиб балки?

Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

ν-прогиб сечения C; θ-угол поворота сечения C.

Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости.

Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет.

Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Метод начальных параметров

Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)

Под начальными параметрами понимаются уже известные перемещения:

• в опорах прогибы равны нулю;
• в жесткой заделке прогиб и угол поворота сечения равен нулю.

Расчет прогибов балки

Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

Реакции опор

Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.

Система координат

Далее вводим систему координат, с началом в левой части балки (точка А):

Распределенная нагрузка

Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.

https://www.youtube.com/watch?v=uxnNg1vN0SY

Если бы нагрузка была приложена вот таким способом:

То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.

Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:

Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
[ { V }_{ A }=0quad приquad x=0 ] [ { V }_{ B }=0quad приquad x=8м ]

Записываем уравнение метода начальных параметров для сечения C:

[ E{ I }_{ z }{ V }_{ C }=… ]

Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:

[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … ]

Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:

[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ heta }_{ A }cdot 4+… ]

Учет внешней нагрузки

И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. Здесь есть несколько особенностей:

• Сосредоточенные силы и распределенные нагрузки, которые направленны вверх, то есть совпадают с направлением оси y, в уравнении записываются со знаком «плюс». Если они направленны наоборот, соответственно, со знаком «минус»:

• Моменты, направленные по часовой стрелке – положительные, против часовой стрелки – отрицательные:

• Все сосредоточенные моменты нужно умножать дробь:

[ Mcdot frac { { x }{ 2 } }{ 2 } ]

• Все сосредоточенные силы нужно умножать дробь:

[ Fcdot frac { { x }{ 3 } }{ 6 } ]

• Начало и конец распределенных нагрузок нужно умножать на дробь:

[ qcdot frac { { x }{ 4 } }{ 24 } ]

Формулы прогибов

С учетом всех вышеописанных правил запишем окончательное уравнение для сечения C:

[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ heta }_{ A }cdot 4+frac { { R }_{ A }cdot { 4 }{ 3 } }{ 6 } -frac { Fcdot { 4 }{ 3 } }{ 6 } -frac { qcdot { 2 }{ 4 } }{ 24 } ]

В этом уравнении содержится 2 неизвестные величины – искомый прогиб сечения C и угол поворота сечения A.

Поэтому, чтобы найти прогиб, составим второе уравнение для сечения B, из которого можно определить угол поворота сечения A. Заодно закрепим пройденный материал:

[ E{ I }_{ z }{ V }_{ B }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ heta }_{ A }cdot 8+frac { { R }_{ A }cdot { 8 }{ 3 } }{ 6 } -frac { Fcdot { 8 }{ 3 } }{ 6 } -frac { qcdot 6{ 4 } }{ 24 } +frac { qcdot 2{ 4 } }{ 24 } =0 ]

Упрощаем уравнение:

[ E{ I }_{ z }{ heta }_{ A }cdot 8+874.67=0 ]

Выражаем угол поворота:

[ { heta }_{ A }=-frac { 874.67 }{ 8E{ I }_{ z } } =-frac { 109.33кН{ м }{ 2 } }{ E{ I }_{ z } } ]

Подставляем это значение в наше первое уравнение и находим искомое перемещение:

[ E{ I }_{ z }{ V }_{ C }=frac { -109.33cdot 4E{ I }_{ z } }{ E{ I }_{ z } } +frac { { R }_{ A }cdot { 4 }{ 3 } }{ 6 } -frac { Fcdot { 4 }{ 3 } }{ 6 } -frac { qcdot { 2 }{ 4 } }{ 24 } =-frac { 280кН{ м }{ 3 } }{ E{ I }_{ z } } ]

Вычисление прогиба

Значение получили в общем виде, так как изначально не задавались тем, какое поперечное сечение имеет рассчитываемая балка. Представим, что металлическая балка имеет двутавровое поперечное сечение №30. Тогда:

[ { V }_{ C }=-frac { 280кН{ м }{ 3 } }{ E{ I }_{ z } } =-frac { 280cdot { 10 }{ 9 }Нcdot { см }{ 3 } }{ 2cdot { 10 }{ 7 }frac { Н }{ { см }{ 2 } } cdot 7080{ см }{ 4 } } =-2см ]

Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.