Максимально допустимый прогиб металлической балки

Как рассчитать деревянную балку

В частном домостроении есть 3 вида конструкций, которые необходимо подбирать по расчету. Это фундамент, перекрытие и крыша. Конечно, вы можете сделать это и без расчета, опираясь на свой опыт или из опыт своих друзей и знакомых.

Но тогда вы рискуете своей безопасностью или своим «кошельком». Другими словами, конструкции могут не выдержать тех нагрузок, которые на них приходятся, или они возводятся с большой надежностью, чем требуется, и на это идут лишние деньги.

Ниже мы рассмотрим, как можно рассчитать деревянную балку, т.е. подобрать ее оптимальное сечение в зависимости от условий эксплуатации и характеристики материала.

Расчет балок должен происходить в следующей последовательности:

1. Сбор нагрузок на балку.

Сбор нагрузок — это та процедура, без которой не обходится ни один расчет. Процедура эта довольно длинная, поэтому она вынесена в отдельную статью, где приведен пример сбора нагрузок на перекрытие и балку.

Для тех же, кому нужно рассчитать балку междуэтажного или чердачного перекрытия и кто не хочет заниматься сбором нагрузок, существует универсальный метод. Он заключается в том, что для междуэтажного перекрытия можно принять расчетную нагрузку равную 400 кг/м2, а для чердачного — 200 кг/м2.

Но иногда эти нагрузки могут быть сильно завышены. Например, когда строится небольшой дачный домик, на втором этаже которого будут располагаться две кровати и шкаф, нагрузку можно взять и 150 кг/м2. Только это исключительно на Ваше усмотрение.

2. Выбор расчетной схемы.

3. Определение требуемого момента сопротивления.

Это так называемый расчет по первой группе предельных состояний — по несущей способности (прочности и устойчивости). Здесь определяется минимальное допустимое сечение деревянной балки, при котором эксплуатация конструкций будет происходить без риска наступления их полной непригодности к эксплуатации.

Примечание: в расчете используются расчетные нагрузки.

4. Определение максимально допустимого прогиба балки.

Это расчет по второй группе предельных состояний — по деформациям (прогибу и перемещениям). По данному расчету определяется сечение деревянной балки в зависимости о предельного прогиба, при превышении которого будет нарушена нормальная их эксплуатация.

Примечание: в расчет используются нормативные нагрузки.

Теперь конкретнее. Для того, чтобы рассчитать деревянную балку перекрытия, Вы можете воспользоваться специальным калькулятором или примером ниже.

Пример расчета деревянной балки перекрытия.

Расчет выполняется в соответствии со СНиП II-25-80 ( СП 64.13330.2011) «Деревянные конструкции» [1] и применением таблиц [2].

Исходные данные

Требуется рассчитать балку междуэтажного перекрытия над первым этажом в частном доме.

Материал — дуб 2 сорта.

Срок службы конструкций — от 50 до 100 лет.

Состав балки — цельная порода (не клееная).

Шаг балок — 800 мм;

Длина пролета — 5 м (5 000 мм);

Пропитка антипиренами под давлением — не предусмотрена.

Расчетная нагрузка на перекрытие — 400 кг/м2; на балку — qр = 400·0,8 = 320 кг/м.

Нормативная нагрузка на перекрытие — 400/1,1 = 364 кг/м2; на балку — qн = 364·0,8 = 292 кг/м.

Расчет

1) Подбор расчетной схемы.

Так как балка опирается на две стены, т.е. она шарнирно оперта и нагружена равномерно-распределенной нагрузкой, то расчетная схема будет выглядеть следующим образом:

2) Расчет по прочности.

Определяем максимальный изгибающий момент для данной расчетной схемы:

Мmax = qp·L2/8 = 320·52/8 = 1000 кг·м = 100000 кг·см,

где: qp — расчетная нагрузка на балку;

L — длина пролета.

Определяем требуемый момент сопротивления деревянной балки:

Wтреб = γн/о·Mmax/R = 1,05·100000/121,68 = 862,92 см3,

где: R = Rи·mп·mд·mв·mт·γсc = 130·1,3·0,8·1·1·0,9 = 121,68 кг/см2 — расчетное сопротивление древесины, подбираемое в зависимости от расчетных значений для сосны, ели и лиственницы при влажности 12% согласно СНиП [1] — таблицы 1 [2] и поправочных коэффициентов:

mп = 1,3 — коэффициент перехода для других пород древесины, в данном случае принятый для дуба (таблица 7 [2]).

mд = 0,8 — поправочный коэффициент принимаемый в соответствии с п.5.2. [1], вводится в случае, когда постоянные и временный длительные нагрузки превышают 80% суммарного напряжения от всех нагрузок.

mв = 1 — коэффициент условий работы (таблица 2 [2]).

mт = 1 — температурный коэффициент, принят 1 при условии, что температура помещения не превышает +35 °С.

γсс = 0,9 — коэффициент срока службы древесины, подбирается в зависимости от того, сколько времени вы собираетесь эксплуатировать конструкции (таблица 8 [2]).

γн/о = 1,05 — коэффициент класса ответственности. Принимается по таблице 6 [2] с учетом, что класс ответственности здания I.

В случае глубокой пропитки древесины антипиренами к этим коэффициентам добавился бы еще один: ma = 0.9.

Примечание: перечисленные таблицы вы можете найти здесь.

Определение минимально допустимого сечения балки:

Так как чаще всего деревянные балки перекрытия имеют ширину 5 см, то мы будем находить минимально допустимую высоту балки по следующей формуле:

h = √(6Wтреб/b) = √(6·862,92/5) = 32,2 см.

Формула подобрана из условия Wбалки = b·h2/6. Получившийся результат нас не удовлетворяет, так как перекрытие толщиной более 32 см никуда не годится. Поэтому увеличиваем ширину балки до 10 см.

h = √(6Wтреб/b) = √(6·862,92/10) = 22,8 см.

Принятое сечение балки: bxh = 10×25 см.

3) Расчет по прогибу.

Здесь мы находим прогиб балки и сравниваем его с максимально допустимым.

Определяем прогиб принятой балки по формуле соответствующей принятой расчетной схеме:

f = (5·qн·L4)/(384·E·J) = (5·2,92·5004)/(384·100000·13020,83) = 1,83 см

где: qн = 2,92 кг/cм — нормативная нагрузка на балку;

L = 5 м- длина пролета;

Е = 100000 кг/см2 — модуль упругости. Принимается равным в соответствии с п.5.3 СП 64.13330.2011 вдоль волокон 100000 кг/см2 и 4000 кг/см2 поперек волокон не взирая на породы при расчете по второй группе предельных состояний.

Но справедливости ради нужно отметить, что модуль упругости в зависимости от влажности, наличия пропиток и длительности нагрузок только у сосны может колебаться от 60000 до 110000 кг/см2.

Поэтому, если вы хотите перестраховаться, то можете взять минимальный модуль упругости.

J = b·h3/12 = 10·253/12 = 13020,83 см4 — момент инерции для доски прямоугольного сечения.

Определяем максимальный прогиб балки:

fmax = L·1/250 = 500/250 = 2,0 см.

Предельный прогиб определяется по таблице 9 [2], как для междуэтажных перекрытий.

Сравниваем прогибы:

Вывод: балка сечением bxh = 10×25 см полностью удовлетворяет условиям по прочности и прогибу.

статьей с друзьями:

Максимально допустимый прогиб металлической балки

В частном домостроении есть 3 вида конструкций, которые необходимо подбирать по расчету. Это фундамент, перекрытие и крыша. Конечно, вы можете сделать это и без расчета, опираясь на свой опыт или из опыт своих друзей и знакомых.

Но тогда вы рискуете своей безопасностью или своим «кошельком». Другими словами, конструкции могут не выдержать тех нагрузок, которые на них приходятся, или они возводятся с большой надежностью, чем требуется, и на это идут лишние деньги.

Ниже мы рассмотрим, как можно рассчитать деревянную балку, т.е. подобрать ее оптимальное сечение в зависимости от условий эксплуатации и характеристики материала.

Расчет балок должен происходить в следующей последовательности:

1. Сбор нагрузок на балку.

Сбор нагрузок — это та процедура, без которой не обходится ни один расчет. Процедура эта довольно длинная, поэтому она вынесена в отдельную статью, где приведен пример сбора нагрузок на перекрытие и балку.

Для тех же, кому нужно рассчитать балку междуэтажного или чердачного перекрытия и кто не хочет заниматься сбором нагрузок, существует универсальный метод. Он заключается в том, что для междуэтажного перекрытия можно принять расчетную нагрузку равную 400 кг/м2, а для чердачного — 200 кг/м2.

Но иногда эти нагрузки могут быть сильно завышены. Например, когда строится небольшой дачный домик, на втором этаже которого будут располагаться две кровати и шкаф, нагрузку можно взять и 150 кг/м2. Только это исключительно на Ваше усмотрение.

2. Выбор расчетной схемы.

3. Определение требуемого момента сопротивления.

Это так называемый расчет по первой группе предельных состояний — по несущей способности (прочности и устойчивости). Здесь определяется минимальное допустимое сечение деревянной балки, при котором эксплуатация конструкций будет происходить без риска наступления их полной непригодности к эксплуатации.

Примечание: в расчете используются расчетные нагрузки.

4. Определение максимально допустимого прогиба балки.

Это расчет по второй группе предельных состояний — по деформациям (прогибу и перемещениям). По данному расчету определяется сечение деревянной балки в зависимости о предельного прогиба, при превышении которого будет нарушена нормальная их эксплуатация.

Примечание: в расчет используются нормативные нагрузки.

Теперь конкретнее. Для того, чтобы рассчитать деревянную балку перекрытия, Вы можете воспользоваться специальным калькулятором или примером ниже.

Расчет металлической балки на прогиб: учимся составлять формулы

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Что такое прогиб балки?

Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

ν-прогиб сечения C; θ-угол поворота сечения C.

Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет.

Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Метод начальных параметров

Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)

Под начальными параметрами понимаются уже известные перемещения:

• в опорах прогибы равны нулю;
• в жесткой заделке прогиб и угол поворота сечения равен нулю.

Расчет прогибов балки

Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

Исходные данные для расчетов

Для каркаса потолочных перекрытий малогабаритных частных домов обычно используется двутавр 10 – 20 номеров. Характеристики этих профилей приводятся в ГОСТ 8239-72 – их линейные размеры, площади сечения, максимальные моменты сопротивления по вертикали Wy и минимальные моменты инерции Jy.

Необходимо знать тип плит, которые будут опираться на балочный каркас, а также размеры несущего периметра дома. Можно применить пустотные железобетонные плиты ПК-12-10-8 (1180 х 990 мм, масса 380 кг), а размеры дома взять 4,5 х 6 м.

Балки укладываются вдоль короткой стены; шаг укладки при таком размере плит равен 1000 мм (стыки плит совпадают с продольными осями балок, при минимальном зазоре 1 см).

Это потребуется для расчета распределенной нагрузки, и исходя из нее – линейной нагрузки на балку, вес самой балки по сравнению с распределенной нагрузкой мал, и при вычислении линейной нагрузки им можно пренебречь.

Распределенная нагрузка при таком типе плит будет равна 325 кгс / м2. К этому надо добавить нагрузку возможных перегородок на верхней стороне перекрытия (75 кгс / м2) и возможную временную нагрузку (200 кгс / м2). В итоге нагрузка, распределенная по площади:

Q = 325 + 75 + 200 = 600 кгс / м2,

а линейная нагрузка

q = Q * p = 600 кгс / м = 6 кгс / см.

Эта величина используется в дальнейших расчетах.

Расчет на прогиб

Изгибающий момент для каждой балки вычисляется, исходя из величины линейной нагрузки q, шага укладки балок p и длины перекрываемого пролета L. Так как балки укладываются вдоль короткой стороны, то L = 4,5 м = 450 см (конечно, сами балки длиннее – около 5 м, так как опираются на стены, но шарнирными опорами для них служат именно внутренние края стен).

Искомая величина момента, в таком случае:

My = (q * L2) / 8 = 6 * 4502 / 8 = 151875 кгс * см.

Максимальный момент сопротивления сечения балки можно рассчитать, разделив изгибающий момент на расчетное сопротивление стали – например, марки С235, равное 2150 кгс / см2:

Wy = 151875 / 2150 = 70,6 см3.

Это полученное значение надо сравнить с величиной момента сопротивления сечения двутавровой балки. Из таблицы ГОСТ 8239-72 видно, что вычисленный показатель  примерно соответствует (с запасом) моменту сопротивления для профиля 14 (81,7 см3). Следовательно, этот номер проката будет удовлетворять требованиям к прочности балок.

Расчет на жесткость

Жесткость балок характеризуется максимальной величиной прогиба при заданных исходных параметрах. В случае распределенной нагрузки прогиб вычисляется по формуле:

f = 5 * q * L4 / (384 * E * Jy), где

• q – линейная нагрузка на балку;
• L – длина пролета;
• E – модуль упругости материала, для стали С235 равный 2,1 * 106 кгс / см2;
• Jy – минимальный момент инерции для данного профиля.

Для принятых ранее исходных данных, с учетом того, что из расчета на прочность наиболее подходящим профилем оказался № 14, для которого Jy, по табличным значениям ГОСТ, равен 572 см4, можно получить:

f = 2,6 см,

а в относительной мере, с учетом того, что длина пролета 450 см – 1 / 172. Это превышает максимально допустимый прогиб, принятый равным 1 / 250.

Поэтому расчет приходится повторить и вычислить прогиб для другого номера проката. Для № 16, у которого момент инерции равен 873 см4, абсолютный прогиб получается 1,74 см, а относительный – 1 / 256, что является приемлемым.

Итоги расчета

Итак, для помещения размером 4,5 х 6 м каркас потолочного перекрытия из железобетонных плит ПК-12-10-8 с распределенной нагрузкой 600 кгс / м2 может быть устроен из двутавровых балок профиля № 16 стали марки С235, расположенных вдоль короткой стороны с шагом 1 м. Можно рассчитать, что для такого здания понадобится 7 таких балок длиной по 5 м, и, зная массу и цену погонного метра, вычислить общую массу балочного каркаса и его стоимость.

Так, для приведенного примера общее количество погонных метров – 35; масса балочного каркаса из профиля № 16 – 525 кг.

Проверка прогибов стальной балки

При расчете стальных балок по II-й ГПС (по прогибам) необходимо создавать раскрепления для прогибов:

Информация из справки LIRA SAPR (СправкаПояснения СтальПроверки прогибов):

Проверка прогиба осуществляется сопоставлением реально определенного относительного прогиба (L/f) с максимально возможным для данного конструктивного элемента прогибом.

В данной версии проверка выполняется только для балок на основании состава загружений во всех сочетаниях. Учитываются коэффициенты надежности по нагрузке (заданные при формировании РСУ в среде ПК ЛИРА-САПР) и коэффициенты сочетания.

Перемещения, вызванные загружениями с долей длительности 0, в данном расчете не используются.

Прогибы находятся для каждого сечения на основании распределения MY1, MZ1, QY1, QZ1 по длине элемента. Соответственно, увеличение количества расчетных сечений способствует более точному определению прогибов (особенно, если воздействуют сосредоточенные силовые факторы).

Важно: Предусмотрена возможность определять не чистые перемещения (относительно локальных осей Y и Z в недеформированной схеме), а прогиб относительно двух выбранных условно неподвижных точек – точек раскрепления (в случае консоли, например, относительно одной точки).

Схема к определению прогибов балки с раскреплениями и без раскреплений

На приведенном фрагменте показан механизм определения прогибов (они обозначены как di и dk) в конструктивном элементе с наложенными раскреплениями на элементы.

Если раскрепления не наложены, то прогиб принимается равным полному расстоянию до оси X.

Важно: Если балка (ригель) разбита по длине промежуточными узлами, то для нее необходимо создать конструктивный элемент и раскрепления для проверки прогибов создавать как для конструктивного элемента (т.е. для балки как единого целого).

В расчете стальных конструкций коэффициент расчетной длины (и для балок, и для колонн, и для ферм) применяется к длине конечного элемента (КЭ), если не задан конструктивный элемент (КоЭ).

Если задан КоЭ, то коэффициент расчетной длины применяется к полной длине КоЭ.

Расчётная модель рамы с цельным ригелем и разбитым на отдельные элементы

Согласно нормативной документации прогиб определяется от действия нормативных нагрузок. Поскольку в LIRA SAPR все нагрузки прикладываются к узлам и элементам их расчётными значениями, при определении прогибов программа определяет нормативное значение нагрузок путём деления их на коэффициент надёжности.

Посмотреть какие приняты коэффициенты надёжности, а также ввести их вручную, если это необходимо, можно в окне параметров расчёта.

Мозаика результатов проверки назначенных сечений по 2 предельному состоянию

Предельно допустимый L/200=6000/200=30мм

Без задания раскреплений (по абсолютному перемещению узлов балки):
((39,8мм/ к-т надежности по нагрузке)/ 30мм))*100%=((39,8/1,1)/30)*100%=120,6%

С заданием раскреплений (по относительному перемещению узлов балки за вычетом перемещений опорных узлов):
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%

Расчёт прогибов стрельчатой арки

Пример — рама переменного сечения (РПС) пролётом 18 м. Соединение полурам в коньке — шарнирное, опирание полурам на фундамент — шарнирное.

Расчётная модель рамы

При этом в параметрах «Дополнительные характеристики» необходимо указать вручную пролет, с которым программа будет сравнивать прогиб (автоматическое определение пролета возможно только для линейных балок, где все конечные элементы (КЭ) конструктивного элемента (КоЭ) лежат на одной оси):

Эпюра перемещений fz ригеля одной полурамы (вдоль местной оси Z1 стержня)

Мозаика перемещений узлов по Z и «Раскрепления для прогибов» (раскреплён только ригель №4)

Результаты определения прогибов в СТК-САПР:

Результаты определения прогибов ригелей №2 и №4

Предельно допустимый L/200=17664/200=88.32 мм

Без задания раскреплений (по абсолютному значению на эпюре прогибов fz):
96.7/17644=1/182 — совпадает с результатом расчёта элемента №2

С заданием раскреплений (по относительному значению на эпюре прогибов fz):
(96.7-(-6.46))/17644=1/171 — совпадает с результатом расчёта элемента №4

Без задания раскреплений (по абсолютному значению перемещений узлов):
99.8/17644=1/177 — не совпадает ни с чем

Вывод: Расчёт на прогибы выполняется в местной системе координат стержня. Прогиб стрельчатых и цилиндрических арок, а также любых криволинейных конструкций, нужно определять по перемещениям узлов в глобальной системе координат и вручную сравнивать с предельно допустимыми значениями.

Пример – цилиндрическая арка пролётом 18 м, стрелой подъёма f = 9 м. Соединение всех элементов между собой — жёсткое, опирание на фундамент — шарнирное.

Нагрузки на арку приложены их расчётными значениями. Значения нагрузок для определения прогибов принимаются согласно СП 20.13330.2016 Нагрузки и воздействия, таблица Д.1 Приложения Д.

В данном примере арка является конструкцией покрытия, прогиб которой должен определяться от постоянных и длительных нагрузок (п.2 табл. Д.1). Для визуализации перемещений от нормативных значений нагрузок, необходимо создать особое РСН с нормативными длительными значениями нагрузок.

Загружение 1 — постоянное, коэффициент надёжности 1.1;
Загружение 2 — кратковременное, коэффициент надёжности 1.2, доля длительности 0.35;

Вычислим коэффициенты для перехода к нормативным значениям

Загружение 1 Kn=1/1.1=0.91;
Загружение 2 Kn=1/1.2*0.35=0.292

Таблица РСН с сочетаниями расчётных и нормативных значений нагрузок с учётом длительности.

Мозаика перемещений узлов цилиндрической арки от РСН2

Предельно допустимый прогиб L/200=18000/200=90 мм

Фактический прогиб (по абсолютному значению перемещений узлов): 32.2/18000=1/559 – меньше предельно допустимого значения.

Примечание: если подобная конструкция стоит на своих опорах, то перемещения опорных точек (для получения относительных перемещений) удобно получить через «Мозаику относительных перемещений», указав реперный узел.

Мозаика перемещений узлов в глобальной СК (абсолютных)

Мозаика перемещений узлов в глобальной СК относительно реперного узла

Полный расчет балки на прочность и жесткость

Задача

Произвести полный расчет на прочность и проверить жесткость изгибаемой статически определимой двутавровой балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [σ]=160 МПа и [τ]=100 МПа, допустимый прогиб балки [f]=l/400

Решение

Определение опорных реакций

Подробно пример определения опорных реакций для балки рассмотрен здесь

Из Σmв=0

Из ΣmА=0

Построение эпюр Q и М

Примеры построения эпюр поперечных сил Q и изгибающих моментов M для балки

В пролете балки 0 ≤ z2 ≤ l

QII= — RB+ qz2= -52+30∙z2QII(z=0)= -52 кН

QII(z=l)= -52+30∙4=68 кН

MII=RB∙z2-qz22/2=52z2-30∙z22/2MII (z=0)= 0

MII (z=l)= -32 кНм

На консоли l ≤ z1≤ (l+a)

QI= — RB+ ql — RA=-52+30∙4-108=-40 кН

MI=RB z1-ql(z1-l/2)+RA(z1-l)=52z1-30∙4(z1-4/2)+108(z1-4)MI (z=l)= -32 кНм

MI (z=l+a)= 0

По этим данным построены эпюры Q и М.

Подбор сечения двутавровой балки

Так как Мmах = 45 кНм, то

Wx≥Mmax / [σ] = 45∙103 / 160∙106= 0,281 м3= 281 см3.

Расчет балок на прогиб. Максимальный прогиб балки: формула

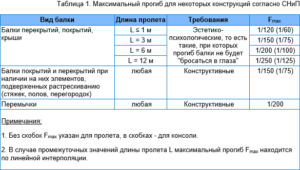
Балка – элемент в инженерии, представляющий собой стержень, который нагружают силы, действующие в направлении, перпендикулярном стержню. Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.

Типы

На сегодняшний день в строительстве могут использоваться балки, изготовленные из разных материалов. Это может быть металл или дерево. Каждый конкретный случай подразумевает под собой разные балки. При этом расчет балок на прогиб может иметь некоторые отличия, которые возникают по принципу разницы в строении и используемых материалов.

Деревянные балки

Сегодняшнее индивидуальное строительство подразумевает под собой широкое применение балок, изготовленных из дерева. Практически каждое строение содержит в себе деревянные перекрытия. Балки из дерева могут использоваться как несущие элементы, их применяют при изготовлении полов, а также в качестве опор для перекрытий между этажами.

Ни для кого не секрет, что деревянная, так же как и стальная балка, имеет свойство прогибаться под воздействием нагрузочных сил. Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.

Допустимый прогиб балки формируется из двух факторов:

• Соответствие прогиба и допустимых значений.
• Возможность эксплуатации здания с учетом прогиба.

Проводимые при строительстве расчеты на прочность и жесткость позволяют максимально эффективно оценить то, какие нагрузки сможет выдерживать здание в ходе эксплуатации.

Также эти расчеты позволяют узнать, какой именно будет деформация элементов конструкции в каждом конкретном случае.

Пожалуй, никто не будет спорить с тем, что подробные и максимально точные расчеты – это часть обязанностей инженеров-строителей, однако с использованием нескольких формул и навыка математических вычислений можно рассчитать все необходимые величины самостоятельно.

Обратите ваше внимание на то, что для проведения таких вычислений самостоятельно лучше всего использовать укрупненные расчеты, прибегая при этом к достаточно простым схемам. При этом также рекомендуется делать небольшой запас в большую сторону. Особенно если расчет касается несущих элементов.

Расчет балок на прогиб. Алгоритм работы

На самом деле алгоритм, по которому делается подобный расчет, достаточно прост. В качестве примера рассмотрим несколько упрощенную схему проведения расчета, при этом опустив некоторые специфические термины и формулы. Для того чтобы произвести расчет балок на прогиб, необходимо выполнить ряд действий в определенном порядке. Алгоритм проведения расчетов следующий:

• Составляется расчетная схема.
• Определяются геометрические характеристики балки.
• Вычисляется максимальную нагрузку на данный элемент.
• В случае возникновения необходимости проверяется прочность бруса по изгибающему моменту.
• Производится вычисление максимального прогиба.

Как видите, все действия достаточно просты и вполне выполнимы.

Составление расчетной схемы балки

Для того чтобы составить расчетную схему, не требуется больших знаний. Для этого достаточно знать размер и форму поперечного сечения элемента, пролет между опорами и способ опирания. Пролетом является расстояние между двумя опорами. К примеру, вы используете балки как опорные брусья перекрытия для несущих стен дома, между которыми 4 м, то величина пролета будет равна 4 м.

Вычисляя прогиб деревянной балки, их считают свободно опертыми элементами конструкции. В случае балки перекрытия для расчета принимается схема с нагрузкой, которая распределена равномерно.

Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F.

Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.

Момент инерции

Геометрическая характеристика, которая получила название момент инерции, важна при проведении расчетов на прогиб балки. Формула позволяет вычислить эту величину, мы приведем ее немного ниже.

При вычислении момента инерции нужно обращать внимание на то, что размер этой характеристики зависит от того, какова ориентация элемента в пространстве. При этом наблюдается обратно пропорциональная зависимость между моментом инерции и величиной прогиба.

Чем меньше значение момента инерции, тем больше будет значение прогиба и наоборот. Эту зависимость достаточно легко отследить на практике.

Подсчет момента инерции для балки с прямоугольным сечением производится по формуле:

J=b*h3/12, где:

b – ширина сечения;

h – высота сечения балки.

Вычисления максимального уровня нагрузки

Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей.

Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах.

Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность.

Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м. Также для примера примем расстояние между брусьями перекрытия равным 600 мм. В этом случае нужный нам коэффициент составит 0,6.

В результате вычисления максимальной нагрузки получаем следующий результат: q=(60+250+75)*0,6+18=249 кг/м.

Когда значение получено, можно переходить к расчету максимального прогиба.

Вычисление значения максимального прогиба

Когда проводится расчет балки, формула отображает в себе все необходимые элементы. При этом стоит учитывать, что формула, используемая для расчетов, может иметь несколько иной вид, если расчет проводится для разных типов нагрузок, которые будут оказывать влияние на балку.

Сначала приведем вашему вниманию формулу, используемую для расчета максимального прогиба деревянной балки с распределенной нагрузкой.

f=-5*q*l4/384*E*J.

Обратите внимание, что в данной формуле Е – это постоянная величина, которая получила название модуль упругости материала. Для древесины эта величина равна 100 000 кгс/ м².

Продолжив вычисления с нашими данными, использованными для примера, получим то, что для балки из древесины, сечение которой составляет 0,15х0,2 м, а длина равна 4 м, величина максимального прогиба при воздействии распределенной нагрузки равна 0,83 см.

f=-F*l3/48*E*J, где:

F – сила давления на брус.

Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса. Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.

Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель – установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.

Обратите внимание на то, что балки из двутавра применяются несколько реже в силу их формы. Однако также не стоит забывать, что такой элемент конструкции выдерживает гораздо большие нагрузки, чем уголок или швеллер, альтернативой которых может стать двутавровая балка.

Расчет прогиба двутавровой балки стоит производить в том случае, если вы собираетесь использовать ее в качестве мощного элемента конструкции.

Также обращаем ваше внимание на то, что не для всех типов балок из двутавра можно производить расчет прогиба. В каких же случаях разрешено рассчитать прогиб двутавровой балки? Всего таких случаев 6, которые соответствуют шести типам двутавровых балок. Эти типы следующие:

• Балка однопролетного типа с равномерно распределенной нагрузкой.
• Консоль с жесткой заделкой на одном конце и равномерно распределенной нагрузкой.
• Балка из одного пролета с консолью с одной стороны, к которой прикладывается равномерно распределенная нагрузка.
• Однопролетная балка с шарнирным типом опирания с сосредоточенной силой.
• Однопролетная шарнирно опертая балка с двумя сосредоточенными силами.
• Консоль с жесткой заделкой и сосредоточенной силой.

Металлические балки

Расчет максимального прогиба одинаковый, будь это стальная балка или же элемент из другого материала. Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала.

При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра. Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа.

Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.

Расчет максимального прогиба для балки с двумя опорами

В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.

Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости.

Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.

Прогиб балки на двух опорах на расстоянии z от левой опоры при а ≤ z ≤l

f(z)=(-P*a2*b2)/(6E*J*l)*(2*(l-z)/b+(l-z)/a-(l-z)3/a+b2), где Р – прикладываемая сила, Е – модуль упругости материала, J – осевой момент инерции.

В случае балки с двумя опорами момент инерции вычисляется следующим образом:

J=b1h13/12, где b1 и h1 – значения ширины и высоты сечения используемой балки соответственно.

Заключение

В заключение можно сделать вывод о том, что самстоятельно вычислить величину максимального прогиба балки разных типов достаточно просто.

Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.