Модуль сдвига меди
Модуль сдвига меди
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы.
Другими словами, они подвергаются деформации.
Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой.
Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга.
В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Модуль Юнга
Основные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям.
Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E.
И поэтому на практике значения Е для них приводят в гигаПаскалях (1012Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.
График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
E=α/ε
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.
Виды деформации
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь.
Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Δl = α * (lF) / S
Величину, обратную α, и называют модулем Юнга:
1/α = E
Относительная деформация:
ε = (Δl) / l = α * (F/S)
Отношение растягивающей силы F к S называют упругим напряжением σ:
ε=α σ
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
σ = ε/α = E ε
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / lМодуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.
Инструмент для определения предела прочности
Кроме того, существуют пределы прочности на сжатие материала и на растяжение.
Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления.
В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия.
По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала.
В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно.
Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
Значения σраст в МПа:
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты.
Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности.
Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности.
Он характеризует способность изделия к перегрузкам выше номинальных.
Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.
Запас прочности
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
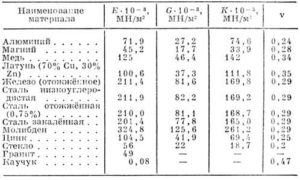
Связь с другими модулями упругости
Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:
E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.
, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Модуль упругости — что это такое? Определение модуля упругости для материалов
Модуль упругости — это физическая величина, которая характеризует упругое поведение материала при приложении к нему внешней силы в конкретном направлении. Под упругим поведением материала подразумевается его деформация в упругой области.
История исследования упругости материалов
Физическая теория упругих тел и их поведения при действии внешних сил была подробно рассмотрена и изучена английским ученым XIX века Томасом Юнгом.
Модуль сдвига меди — Справочник металлиста
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой.
Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга.
В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Модуль Юнга
Модуль Юнга (упругости)
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации.
Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой.
Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р.
Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Модуль Юнга
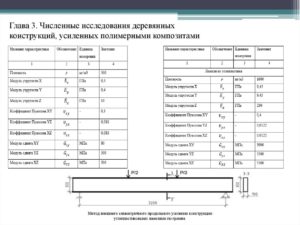
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица). Таблица модуль упругости материалов таблица
Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.
Модуль упругости — что это?
Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.
Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:
- Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
- Модуль сдвига (G), называемый также модулем жёсткости. Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
- Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.
- Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.
Таблица показателей упругости материалов
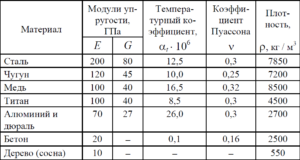
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.
Модуль упругости различных материалов
Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя.
Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему.
Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.
После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.
Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:
- Модуль упругости (Е) для литья, горячекатанной арматуры из сталей марок, именуемых Ст.3 и Ст. 5 равняется 2,1*106 кг/см2.
- Для таких сталей как 25Г2С и 30ХГ2С это значение равно 2*106 кг/см2.
- Для проволоки периодического профиля и холоднотянутой круглой проволоки, существует такое значение упругости, равняющееся 1,8*106 кг/см2. Для холодно-сплющенной арматуры показатели аналогичны.
- Для прядей и пучков высокопрочной проволоки значение равняется 2·10 6 кГ/см2
- Для стальных спиральных канатов и канатов с металлическим сердечником значение равняется 1,5·10 4 кГ/см2, в то время как для тросов с сердечником органическим это значение не превышает1,3·10 6 кГ/см2 .
- Модуль сдвига (G) для прокатной стали равен 8,4·10 6 кГ/см2 .
- И напоследок коэффициент Пуассона для стали равен значению 0,3
Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.
Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).
Сталь и несколько разных её марок
Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному.
Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов.
Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него.
Кстати, если не выражать все значения числовыми отношениями, а взять сразу и посчитать полностью, то эта характеристика стали будет равна: Е=200000 МПа или Е=2 039 000 кг/см2.Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.
Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения.
Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода.
Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.
Способы определения и контроля показателей прочности металлов

Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними.
Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда.
С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
- Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
- Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
- Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
- Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Модуль упругости для разных марок стали
Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Таблица 2: Упругость сталей
| Наименование стали | Значение модуля упругости, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 |
| Сталь 3 | 179…189 |
| Сталь 30 | 194…205 |
| Сталь 45 | 211…223 |
| Сталь 40Х | 240…260 |
| 65Г | 235…275 |
| Х12МФ | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| Р6М5 | 305…320 |
| Р9 | 320…330 |
| Р18 | 325…340 |
| Р12МФ5 | 297…310 |
| У7, У8 | 302…315 |
| У9, У10 | 320…330 |
| У11 | 325…340 |
| У12, У13 | 310…315 |
: закон Гука, модуль упругости.
Модули прочности
Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.
Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.
Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.
Коэффициент Пуассона μ определяет изменения отношение величины относительного сжатия к растяжению. Эта величина зависит только от свойств материала.
Для разных сталей значения указанных модулей приведены в таблице 3.
Таблица 3: Модули прочности для сталей
| Наименование стали | Модуль упругости Юнга, 10¹²·Па | Модуль сдвига G, 10¹²·Па | Модуль объемной упругости, 10¹²·Па | Коэффициент Пуассона, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 | 87…91 | 45…49 | 154…168 |
| Сталь 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Сталь 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Сталь 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Сталь 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65Г | 235…275 | 112…124 | 81…85 | 208…214 |
| Х12МФ | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| Р6М5 | 305…320 | 147…151 | 98…102 | 294…300 |
| Р9 | 320…330 | 155…162 | 104…110 | 301…312 |
| Р18 | 325…340 | 140…149 | 105…108 | 308…318 |
| Р12МФ5 | 297…310 | 147…152 | 98…102 | 276…280 |
| У7, У8 | 302…315 | 154…160 | 100…106 | 286…294 |
| У9, У10 | 320…330 | 160…165 | 104…112 | 305…311 |
| У11 | 325…340 | 162…170 | 98…104 | 306…314 |
| У12, У13 | 310…315 | 155…160 | 99…106 | 298…304 |
Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.